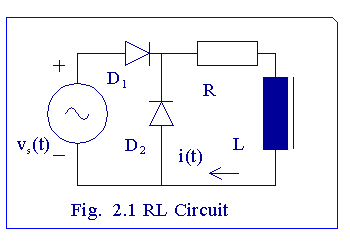
This circuit differs from the half-wave rectifier circuit without a free-wheeling diode. Without a free-wheeling diode, the current through the RL load is disontnuous, but it is  continuous when there is a free-wheeling diode.   Let vs(wt) = E*sin (wt).  When  0 < wt < p, diode D₁ conducts.  When wt  crosses p,  v_s becomes negative for p < wt < 2p.  During this period, the inductor does not discharge its energy back to the source, for there is a path with a lower potential drop through D₂.  When p < wt < 2p, the current through the load decays exponentially.  When the current response becomes periodic, the current at wt = 0 has the same value.  Let the current at wt = 0 be A.

Then

                              A = i(p)*exp [- Rp / (wL)].

Also,   i(wt) = [E/Z] sin (wt - a) + A *exp [- (Rwt)/(wL)], where a  = atan (wL/R) and  Z² = R² + (wL)².

The value of A can be obtained from the above expressions.

E := 340  V

R := 10  W

wL := 10  W

Z := sqrt [(R² + (wL)^2]

Z = 14.142 W

a := atan(wL/R)

a  = 0.785  rad
 

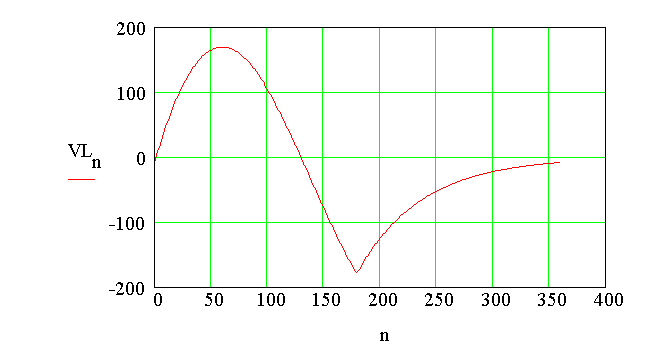
Next the response over a cycle is computed.  An array is created.  The array index corresponding to degrees is converted to radians first. Next the value of load current at wt = p is defined.  Next an array called I_n is created.  I_n is calculated differently, depending on whether the angle is less than or more than 180^o.  The voltage across the inductor is also stored as an array.   Again, it is calculated differently for angle less than 180^o or more.   It is also
shown how the current through each of the diodes can be computed.

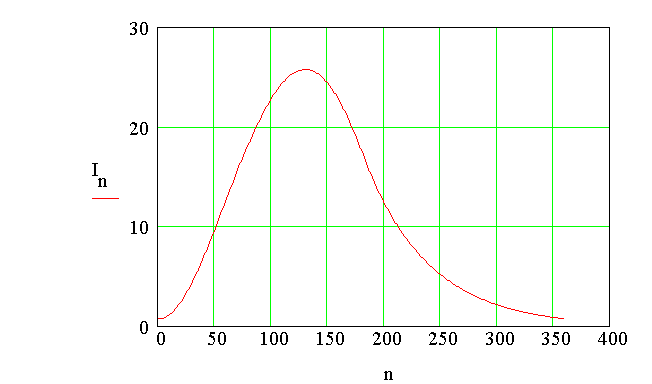
The plot of load current

 

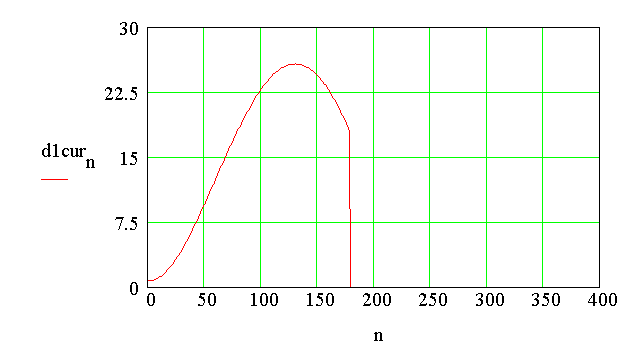
The plot of current through diode D₁

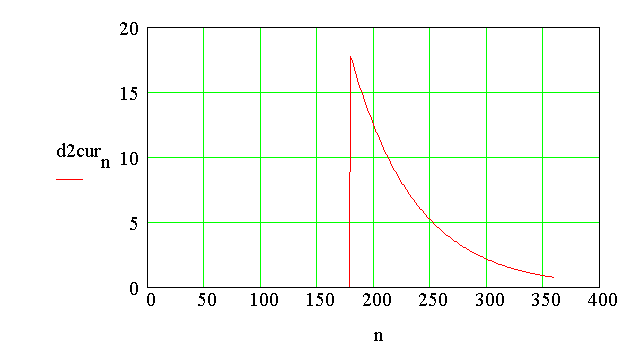
The plot of current through diode D₂

Plot of voltage across the inductor

Next the average and the RMS values of load current are computed. Two

functions are created, one corresponding to angle less than 180^o and

the other corresponding to angle greater than 360^o.

 
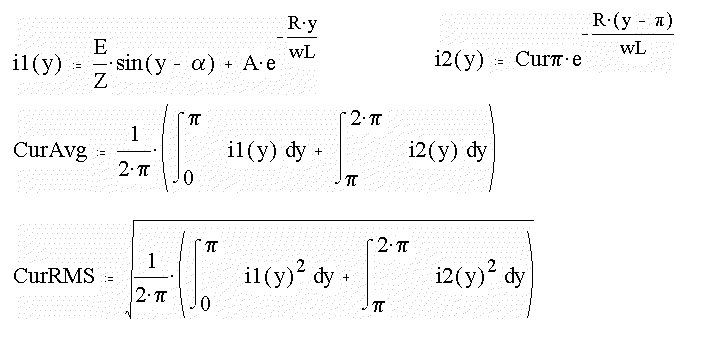
 CurAvg = 10.823 Amp

 CurRMS = 13.952 Amp