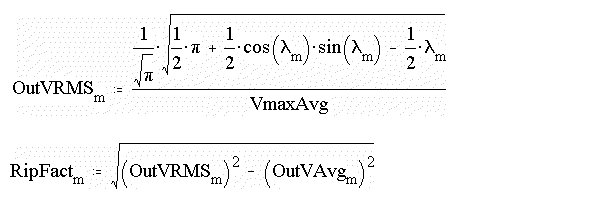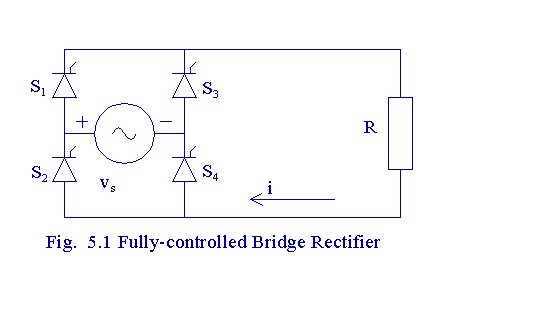
The operation of a fully-controlled bridge rectifier circuit is explained in this program. The load is set to be purely resistive. This bridge rectifier is called as fully-controlled, because all the devices used are SCRs.
 
As the load is purely resistive, the load current waveform follows the load bridge rectifier output voltage waveform.
 
Let us assume that the circuit is switched on at wt = 0 and let the firing angle be a. Let the supply voltage vs(wt) = E sin (wt). When wt = a, the SCRs S1 and S4 get triggered and they start conducting since they are forward-biased. These two SCRs continue to conduct till wt = p. When wt = p radians, the supply voltage falls to zero and the current through the SCRs S1 and S4 falls below the holding level and they cease to conduct. When p <wt < 2p radians, v_s is negative. When v_s is negative, SCRs S1 and S4 are reverse-biased and cannot conduct. However, the SCRs S2 and S3 are forward-biased when v_s is negative and they get triggered when wt = p + a radians and the SCRs S2 and S3 continue to conduct till wt = 2p radians.

During the periods defined by 0 < wt < a, and p < wt < p + a , no SCR is in conduction and the output voltage is zero. The conduction in the load is discontinuous.

 
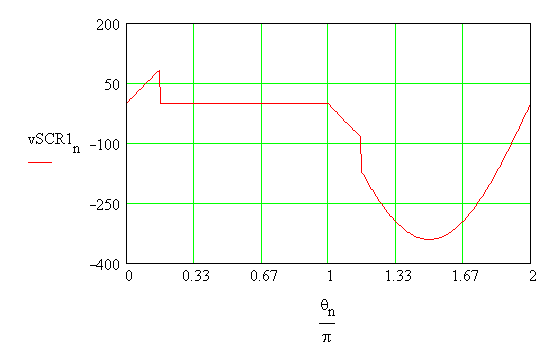
When no SCR is in conduction, it is difficult to define the voltage across each SCR. The voltage source is seen to be connected across the SCRs S1 and S3 are connected in series with back-to-back. If it is assumed that the voltage gets divided between the SCRs equally, we have that the voltage across the
SCR S1 is v_s/2. Then the voltage across the SCR S3 is -v_s/2.  Similarly the voltage across the SCR S4 is vs/2 and the voltage across the SCR S2 is - v_s/2.

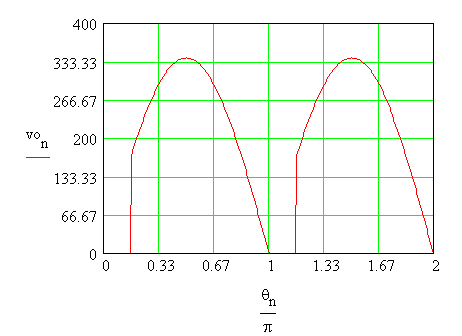
The voltage waveform of the output and the waveform of the voltage across the SCR S1 are obtained and illustrated below. The peak value of the supply voltage is defined as E.

E := 340  V     a : = p/6  rad     n:= 0..360     q_n := (n.p)/180   vs_n := E.sin(q_n )

An expression is obtained in parts, first for the positive half-cycle and then for the other half-cycle.

v1_n := if(q_n < a , 0.0, E.sin(q_n ))

vo_n := if(n<180,v1_n ,v1_n-180 )

An expression for the voltage across the SCR S1 is also obtained in parts.

v2_n := if(q_n < a , vs_n/2 , 0.0)

v3_n := if(q_n < p , v2_n , vs_n/2 )

vSCR1_n := if(q_n < (p+a) , v3_n , vs_n )

 
The output voltage waveform

 
The voltage across the SCR S1

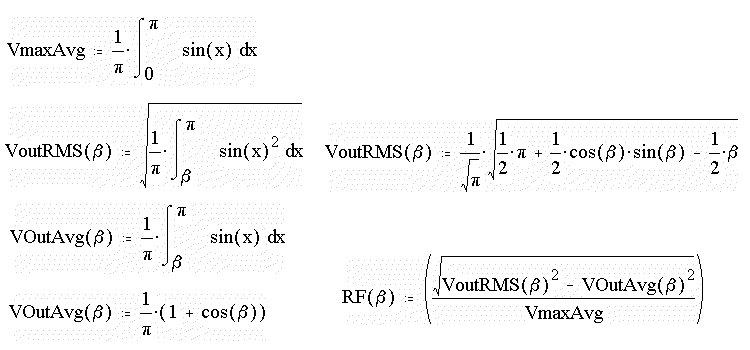
The variation of the output voltage with firing angle can be obtained. At first, the maximum average voltage, which occurs for 0^o firing angle, is derived as a fraction of the peak supply voltage.

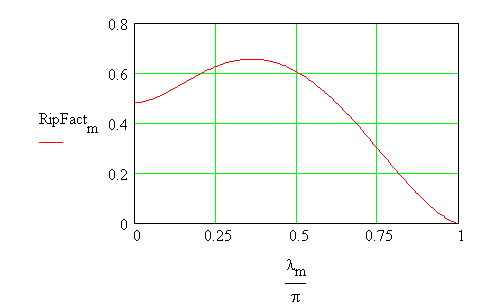
It is seen that the output voltage is not pure d.c., even though a pure d.c. voltage is desirable as output. For a waveform such as the output of the rectifier, a factor of merit, called the ripple factor is defined. The lower the ripple factor is the better the output is. The ripple factor is defined as a function of extinction angle, b and is called RF(b).

In some of the texts, the ripple factor with the denominator as Vo,avg(a), but in this course, the denominator wil be set to be Vo,avg(max). The rms voltage is obtained first and then the ripple factor can be obtained.

These functions can be evaluated numerically as follows. The output voltage and the rms voltage are normalized with respect to the maximum average voltage. The firing angle is called l_m.

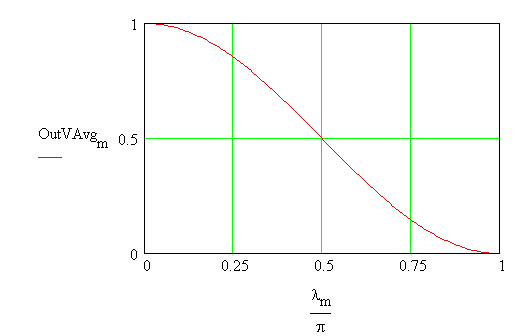
m:= 0..180     l_m := (m.p)/180    OutVAvg_m := [(1 + cos (l_m )]/[(p .VmaxAvg)]

 
 
The Plot of Average Output Voltage as a function of firing angle

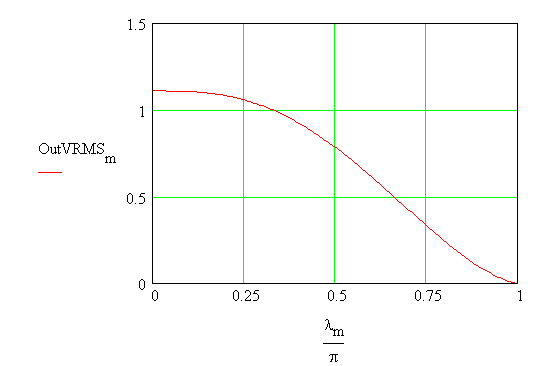
The plot of rms voltage and the ripple factor are obtained as follows

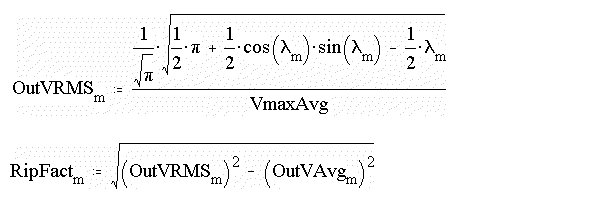
The waveform of current drawn from the supply is illustrated below. When the SCRs S1 and S4 conduct, the supply current is just the load current. But when the SCRs S2 and S3 conduct, the supply current is equal to the load current in magnitude, but of opposite sign.

 
R := 10  W

iL1_n := if(q_n < a , 0.0, (E/R).sin(q_n ))

iL2_n := if(q_n < p+a , 0.0, (E/R).sin(q_n ))

iLine_n := if(n<180,iL1_n ,iL2_n )

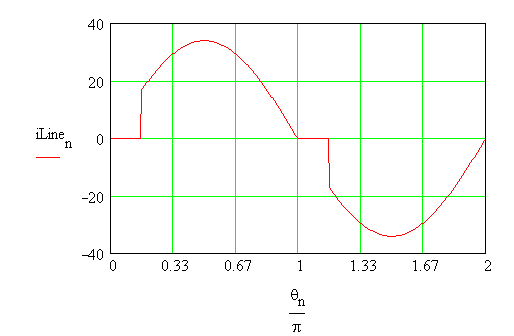
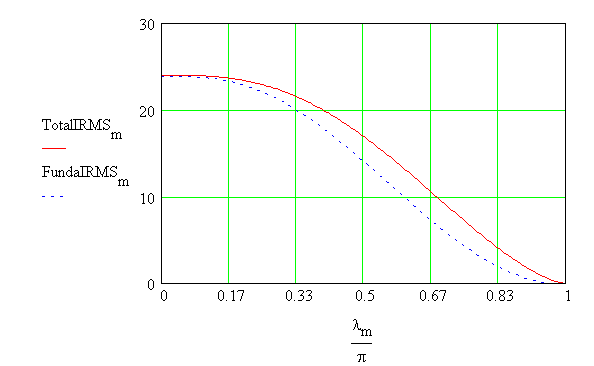
It is seen that the line current is not purely sinusoidal. In such a case, a goodness factor called, the THD (total harmonic distortion) is defined as shown.  In the definition for THD, Irms(a) represents the total rms current and I_rms,1(a) represents the rms value of the fundamental component. The fundamental component is the line frequency component. Here the calculations are carried out as function of the firing angle, set to be l_m.

The variation of THD with the firing angle is obtained as shown.
 

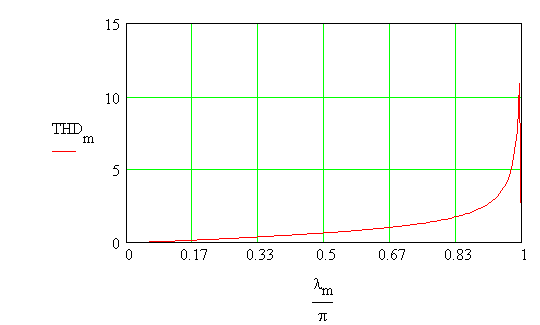
As seen, the THD increases as the firing angle is retarded more and more.