INTRODUCTION
CIRCUIT OPERATION
MATHEMATICAL ANALYSIS
SIMULATION WITH AN APPLET
MATHCAD SIMULATION
SUMMARY

INTRODUCTION

This page describes the operation of the three-phase semi-controlled rectifier. When a semi-controlled rectifier is used, the output of the bridge is controlled when it remains positive. If it tends to become negative, the output is clamped to zero volt through the free-wheeling action of the diodes.

Fig. 1

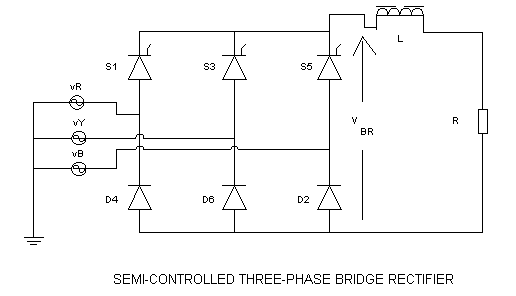
The circuit of the semi-controlled bridge rectifier is shown in Fig. 1, and this circuit contains three-SCRs and three diodes. It is possible to configure the circuit in two more ways. For example, the top-half can contain the diodes and the bottom half the SCRs. Alternatively, six SCRs can be used as in the case of the fully-controlled bridge rectifier and an additional diode can be connected from the negative rail to the positive rail of the bridge, with the anode connected to the negative rail and the cathode to the positive rail. The operation of this circuit is different from that of the circuit displayed above.

CIRCUIT OPERATION

The operation of the semi-controlled rectifier circuit displayed in Fig. 1 is now explained. The waveform of the bridge output voltage for a firing angle of 30o is shown in Fig. 2. .It can be seen that the trace of the positive rail of output voltage is that of a controlled rectifier, since only the top-half of the bridge is controlled. The trace of the bottom rail is that of an uncontrolled bridge rectifier, since the bottom half contains only diodes.

Fig. 2

Let the 3-phase supply be defined as shown in equation (1).

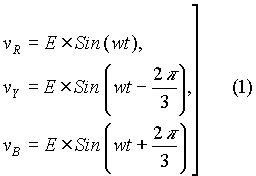
Given that the firing angle is 30^o, SCR S₁ is triggered when wt = 60^o . The conduction range of the SCRs in the top half can be is now expressed in equation (2).

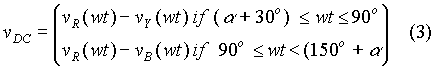
As long as the firing angle a remains less than 60^o, the expression for output voltage over one output cycle can be expressed as follows.

Substituting for v_R, v_Y, and v_B from equation (1), we get that

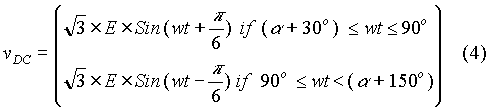
When the firing angle a is higher than 60^o, the expression for output voltage over one output cycle can be expressed as follows, if conduction through the load is continuous.

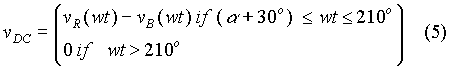
Substituting for v_R, and v_B from equation (1), we get that

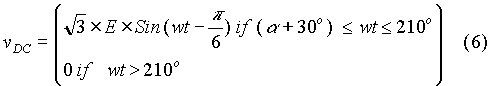
Depending on the firing angle, the bridge output repeats itself every 120^o. The applet shown below plots the output voltage, given the firing angle. It is assumed that conduction through the load impedance is continuous.

Fig. 3

If the firing angle a is less than 60^o, when SCR S₁ is triggered, SCR S₁ and diode D₆ conduct during the period (a + 30^o) £ wt < 90^o. Figure 3 shows the path of conduction that would exist during this period. The pairs that conduct vary depending on the firing angle. Table 1 show the pairs that would conduct when the firing angle a is less than 60^o, whereas Table 2 shows the pairs that would conduct when the firing angle a is greater than 60^o.

MATHEMATICAL ANALYSIS

The aims of anlysis are:

To obtain an expression for the average bridge output voltage as a function of firing angle,
To obtain an expression for the rms bridge output voltage as a function of firing angle,
To obtain an expression for the ripple factor of bridge output voltage as a function of firing angle,
To obtain an expression for the instantaneous load current as a function of firing angle,
To obtain an expression for the instantaneous line current as a function of firing angle,
To obtain an expression for the rms value of the fundamental of line current as a function of firing angle,
To obtain an expression for the rms line current as a function of firing angle,
To obtain an expression for the THD of line current as a function of firing angle,
To carry out harmonic analysis of line current, bridge output voltage and load current at a given firing angle.

TABLE 1: PAIRS IN CONDUCTION WHEN a < 60^o

S₁ – D₆	(a + 30^o) £ wt < 90^o
S₁ – D₂	90^o £ wt < (a + 150^o)
S₃ – D₂	(a + 150^o) £ wt < 210^o
S₃ – D₄	210^o £ wt < (a + 270^o)
S₅ – D₄	(a + 270^o) £ wt < 330^o
S₅ – D₆	330^o £ wt < (a + 390^o)

TABLE 2: PAIRS IN CONDUCTION WHEN a > 60^o

S₁ – D₂	(a + 30^o) £ wt < 210^o
S₁ – D₄	210^o £ wt < (a + 150^o)
S₃ – D₄	(a + 150^o) £ wt < 330^o
S₃ – D₆	330^o £ wt < (a + 390^o)
S₅ – D₆	(a + 270^o) £ wt < 450^o
S₅ – D₂	90^o £ wt < (a + 30^o)

Average Output Voltage

When the conduction through the load is continuous, the average bridge output voltage is obtained as shown below.

Given that the firing angle is less than 60^o,

If the firing angle is greater than 60^o and the conduction is continuous,

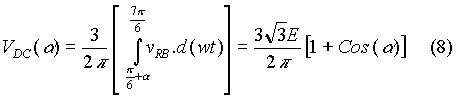
The maximum output voltage occurs when a = 0^o and let it be V_dm:

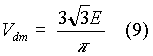
From equation (7) and (9), we obtain that

RMS Output Voltage

The expression for the rms output voltage is found separately for the two cases. The assumption here is that the conduction is continuous. When the firing angle is greater than 60^o,

When the firing angle is less than 60^o,

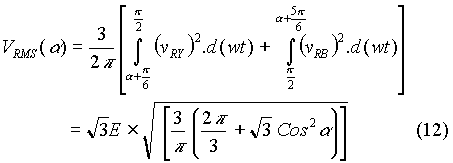
Ripple Factor of the Bridge Output Voltage

The ripple factor, RF(a), of the bridge output voltage can be computed as follows:

Since both V_RMS(a) and V_DC(a) are known, the ripple factor can be computed.

Instantaneous Load Current

An expression for the instantaneous load current as a function of firing angle can be obtained through a somewhat tedious process.

When the firing angle is less than 60^o, the instantaneous bridge output voltage expressed by equation (4) is reproduced below.

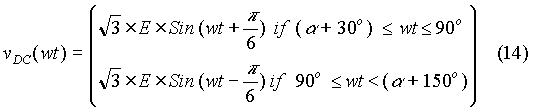
The above expression can be written with the origin shifted to the instant of triggering an SCR. Then

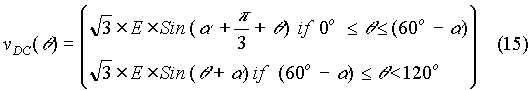
Let the load angle be:

The expression for load current during 0^o £ q £ (60^o – a) can be expressed to be:

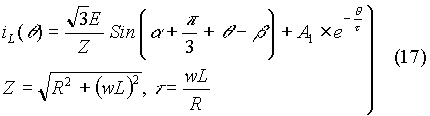
In the expression, A₁ is a constant to be evaluated. Then

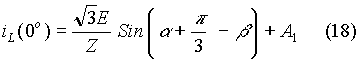
The expression for load current during (60^o – a) £ q £ 120^o can be expressed to be:

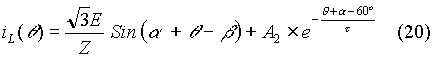
In equation (20), A₂ is a constant to be evaluated. Then

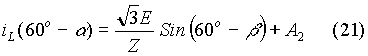
Another expression for the load current can be obtained when the output cycle ends.

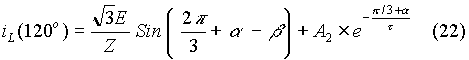
When the load current is periodic, then

From equations (18), (19), (21) , (22) and (23), we can determine A₁ and A₂. From equations (19) and (21), we get that

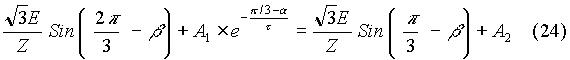
On simplifying the above expression, we get that

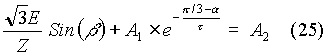
From equations (18), (22) and (23), we get that

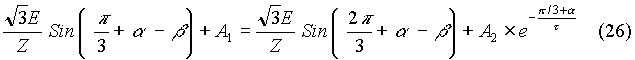
On simplifying the above expression, we get that

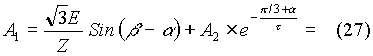
Substituting for A₂ from equation (26),

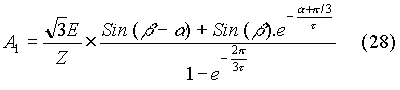
Then A₂ can be determined from equation (25).

Since both A₁ and A₂ are known, the expression for load current has been obtained for the case when the firing angle is less than 60^o.

When the firing angle is greater than 60^o,

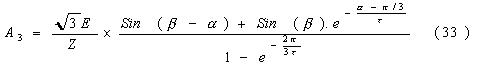
Then the load current can be expressed to be:

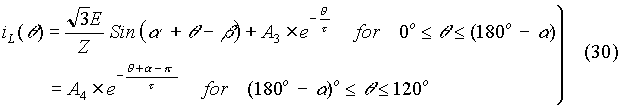
In the above equation, A₃ and A₄ have to be determined. The conditions we have are:

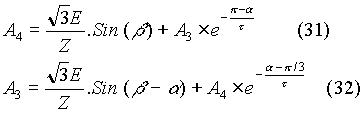
On solving for A₃, we obtain that

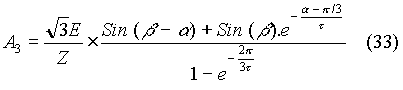
Now an expression for the load current is known for any firing angle.

Instantaneous Load Current

An expression for the instantaneous line current as a function of firing angle can be obtained from the expression for the load current. Here an expression for current through R-phase over an input cycle is obtained with the origin coinciding with the triggering of SCR S₁. When SCR S₁ is in conduction, the line current is equal to the load current Then

When the firing angle is less than 60^o,

When the firing angle is greater than 60^o,

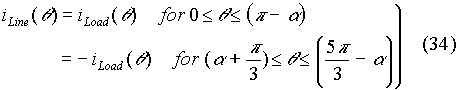
RMS Line Current

Since the line current i_L(q) is known over one input cycle, the rms line current can be obtained.

RMS Value of the Fundamental of Line Current

By performing Fouries series analysis of the line current, the rms value of the fundamental can be obtained. From the rms line current and the rms value of the fundamental of line current, THD can be computed.

SIMULATION WITH AN APPLET

The applet that folows requires two inputs, the firing angle in degrees and the load reactance to resistance ratio, wL/R. Select the response and then click on the RUN button.

MATHCAD SIMULATION

SUMMARY

This page has described the simulation of a semi-controlled three-phase bridge rectifier. Some more topics on controlled rectifier are covered in later pages.

Go to the top of the Page