OPERATION WITH SOURCE INDUCTANCE:
1-PH. CONTROLLED RECTIFIER
CIRCUIT DIAGRAM
CIRCUIT OPERATION
MATHEMATICAL ANALYSIS
SIMULATION
PSPICE SIMULATION
MATHCAD SIMULATION
SIMULATION USING C
SUMMARY 
CIRCUIT DIAGRAM

 

This chapter describes the operation of a single-phase fully- controlled bridge rectifier circuit with a load consisting of both resistance and inductance. In addition, the inductance of ac source supplying power to the circuit is taken into account.

 

CIRCUIT OPERATION
 
The presence of source inductance changes the way the circuit operates during commutation. The word commutation refers to switching conduction from one pair of SCRs to the other. Let vs = E sin wt, with 0  < wt < 360o. Let the load inductance be large enough to maintain a steady current through the load. Let firing angle a be 30o. Let SCRs S2 and S4 be in conduction before wt < 30o. When S1 and S3 are triggered at wt = 30o,  there is current through the source inductance, flowing in the direction opposite to that marked in the circuit diagram and hence commutation of current from S2 and S4 to S1 and S3 would not occur instantaneously. The source current changes from - iL to iL due to the whole of the source voltage being applied across the source inductance. When S1 is triggered with S4 in conduction, the current through S1 would rise from zero to iL and the current through S4 would fall from iL to zero. Similar process occurs with the SCRs S2 and S3. During this period, the current through S3 would rise from zero to iL and , the current through S2 would fall from iL to zero. The duration of the process of commutation is usually referred to as commutation overlap period.
 
The operation of the circuit is illustrated with the help of an animation. There is no scope for setting any variable for animation, since the purpose is only to show how the circuit operates. It is assumed that the load inductance is large to keep the load current at a steady value. You can observe how the currents through the devices and the line current change during commutation overlap. The running of the program can be halted by clicking on the Stop button. It can be resumed by clicking on the Run button. By clicking on the One Step button, you can step through the process. To start or run the process for one more cycle, click on the Start or Repeat button.
MATHEMATICAL ANALYSIS
 
BASED ON THE ASSUMPTION THAT LOAD INDUCTANCE IS INFINITE
 
When the load inductance is infinite, we can assume that the load current is continuous and steady without ripple.  Let the firing angle be a. Let the commutation overlap period last from wt = a till wt = b.
During the period, a < wt <  b, the output voltage is zero because all the SCRs are in conduction. If the SCRs are ideal, the drop across an SCR in conduction is zero and hence the output voltage is zero. During  b < wt < ( p + a),  the output voltage equals E*Sin (wt) and then the average output voltage can be obtained as shown in equation (1).

This expression is not very useful because the value of b is required to be known. The value of a is known, since it is the firing angle, whereas the value of b is not likely to be known.  Here b is the angle at which process of commutation overlap ends and the duration of commutation depends on the firing angle, the value of source reactance and the load impedance and value of b is variable and unknown.  Hence it is preferable to derive an alternate expression. It is possible to derive an alternate expression for the case when the load reactance is large enough to ensure that the load current remains steady without ripple at a given firing angle. Let us assume that the load current be I and the firing angle be a.  Let the line current change from - I to + I during commutation overlap when wt changes from a to b. From the waveforms shown above, the area of volt-seconds lost to output due to commutation overlap is computed as shown in equation (2).

Since this area is lost over p radians, the average value of output voltage lost due to commutation is calculated as shown in equation (3).  It is known that the average output voltage with no commutation overlap is (2E/p)*Cos (a). By subtracting the voltage lost due to commutation, we can get the average output voltage taking into account the effect of commutation overlap, as shown in equation (4).


The waveforms appear as shown below. Key-in a firing angle less than 90o and then press the Start button.
 

 
ANALYSIS WITH A FINITE LOAD INDUCTANCE
 
With a finite load inductance, the conduction through the load can be either continuous or discontinuous. Let angle j be defined as shown in equation (5). If the firing angle a is greater than j, then the current through the load is discontinuous and the analysis is similar to that used for the circuit without a source inductance. When a < j , then the conduction is continuous. The analysis is carried out as follows. In these equations, a is the firing angle, b is the angle at which commutation overlap ends and j has been defined above. Let iL be the load current and is is the source current. Let the source voltage vs = E *Sin (q), where q = wt and 0 < q < 2p . Then the equation that is applicable during b < q < (p + a)  can be expressed as shown in equation (6).  During this period, the line current is equal to load current as defined by equation (7).
During b < q < (p + a), the voltage that appears as output is almost the negative of the source voltage and hence equation (8) is used and the line current has the same magnitude as the load current, but its polarity is opposite to that of load current as indicated by equation (9).
There are two instances of switching in one input cycle and commutation overlap occurs immediately after triggering either pair of SCRs.  The pair consisting of  S1 and S3 is triggered at wt = a and commuation overlap lasts from wt =  a till wt =b  and the output voltage is zero during this period as indicated by equation (10).  Similarly after S2 and S4 are triggered at wt = (p + a), the output voltage is zero from wt = (p + a) till wt = (p + b), as indicated by equation (11).   During the commuation overlap, the entire input voltage is applied across the source inductance, as indicated by equations (12) and (13).
The average and rms output voltage can be obtained as shown by equations (14) and (15).  The maximum output voltage that can occur is indicated by equation (16) neglecting the loss in output that may occur due to commutation overlap.  Then the ripple factor of output voltage can be expressed as shown by equation (17).  If the ripple factor is multiplied by Vom, the rms value of ripple content in output voltage is obtained.
The fundamental component of the source current can be determined and then the THD, DPF and apparent power factor can be determined. The programs for simulation have been based on the equations displayed above.
 
SIMULATION
 
The program in the applet to follow displays the bridge output waveform, the load current, the line current, the voltage across the load inductance, the voltage across the source inductance, the voltage across SCR S1, and the currents through S1 and S4. Key-in the ratio wLL/RL, the ratio wLs/RL and the firing angle in degrees and then click on the Start button.
 
 
The program to follow produces the statistics for this circuit and needs the same inputs as the applet above.

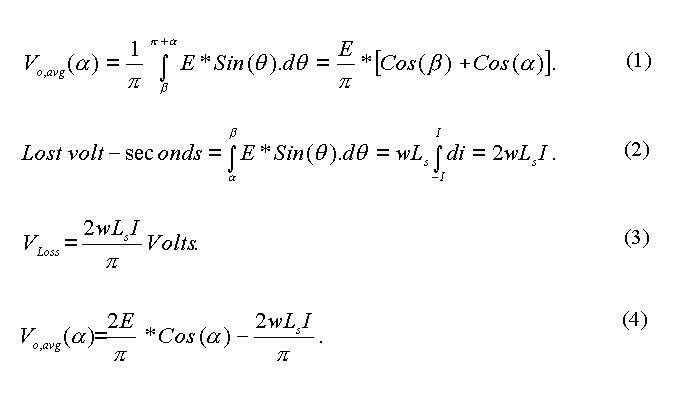
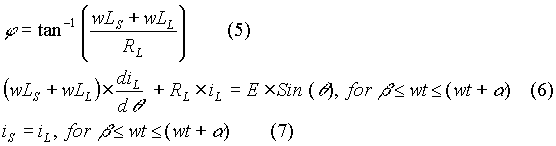
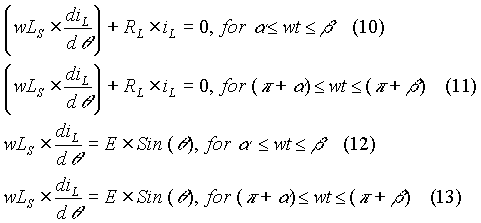
The next applet displays the transient response of the load current. If the load inductance is large, the transient response may last for a few cycles before it settles down to a periodic response. The load current starts building up from zero from the instant one of the pairs of SCRs is triggered first. The response shown starts from this instant.

 

The next applet shows how the average bridge output voltage, the rms output voltage, and the ripple factor vary with firing angle for a given set of wLL/RL and wLs/RL. This program may take some time to run.

 

PSPICE SIMULATION
The circuit used for simulation is presented below.
The Pspice program is presented first.
* Full-wave Bridge Rectifier with RL Load and source Inductance
VIN 9 0 SIN(0 340V 50Hz)
XT1 1 2 5 2 SCR
XT2 0 2 6 2 SCR
XT3 4 0 7 0 SCR
XT4 4 1 8 1 SCR
VP1 5 2 PULSE(0 10 1667U 1N 1N 100U 20M)
VP2 6 2 PULSE(0 10 11667U 1N 1N 100U 20M)
VP3 7 0 PULSE(0 10 1667U 1N 1N 100U 20M)
VP4 8 1 PULSE(0 10 11667U 1N 1N 100U 20M)
L1 2 3 31.8M
L2 1 9 1.6M
R1 3 4 10
R2 1 0 1MEG
R3 2 0 1MEG
R4 4 0 1MEG

* Subcircuit for SCR
.SUBCKT SCR 101 102 103 102
S1 101 105 106 102 SMOD
RG 103 104 50
VX 104 102 DC 0
VY 105 107 DC 0
DT 107 102 DMOD
RT 106 102 1
CT 106 102 10U
F1 102 106 POLY(2) VX VY 0 50 11
.MODEL SMOD VSWITCH(RON=0.0105 ROFF=10E+5 VON=0.5 VOFF=0)
.MODEL DMOD D((IS=2.2E-15 BV=1200 TT=0 CJO=0)
.ENDS SCR
.TRAN 10US 60.0MS 0.0MS 10US
.FOUR 50 V(2,4) I(VIN)
.PROBE
.OPTIONS(ABSTOL=1N RELTOL=.01 VNTOL=1MV)
.END
The waveforms obtained are now presented.
The Voltage Output of the bridge
The Expanded view of Voltage Output of the bridge to show the commutation overlap
The waveform of Load Current
The waveform of line current
The expanded waveform of line current
The waveform of voltage across the line/source inductance
MATHCAD SIMULATION
You can download the MathCad file by clicking on the image below.
You can view the MathCad file by clicking on the image below.
It can be seen that there is close agreement between the results obtained from the Applets and the Mathcad program.

SIMULATION USING C

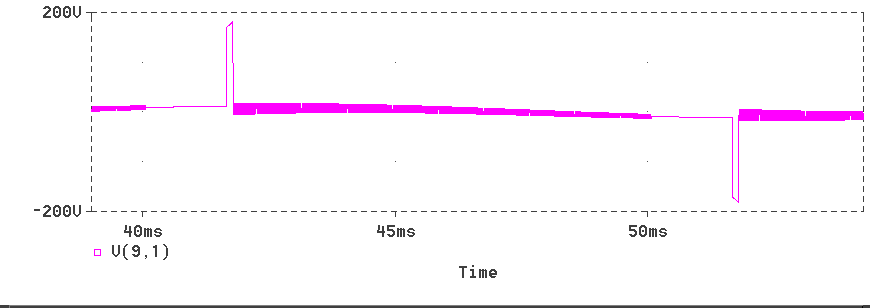
Instead of a Matlab program, a C program is presented below.  You can download this file by clicking on the image displayed below.  This file, called fcb_1pha.cpp, can be complied just as a C program and no feature of C++ has been used in this program.  This program produces an output file called tran_v1.csv and stores in it in the same directory in which the source file is located.  This file can be opened by a spreadsheet program like EXCEL and the plots displayed can be obtained.

C Program
  

// Simulation of a single-phase fully-controlled bridge
// rectifier circuit.
// This program produces the transient response, the periodic
// response. Commuation overlap angle is also computed.
// Calculations normalized.  The average voltage that would
// occur for diode-bridge rectifier with a resistive load is
// taken to be unity.  The average current through the load
// resistor with a pure resistive load on the diode bridge
// rectifier is taken as the unity current.  The parameters to
// be fed are just three: the ratio of load inductive reactance
// to the load resistance, wL1/R , the ratio of source reactance
// to the load resistance to load resistance wL2/R and the firing
// angle in degrees.



#include <math.h>
#include<stdlib.h>
#include<stdio.h>
#include<string.h>
#include<iostream.h>

void kreateRespFile(void);
void tranResponse(void);
void OneCycle(void);
void computeOneStep(void);
void produceEntries(void);


const double pi=3.1415926;
const double deg_rad=pi/180.0;
const double step=pi/720.0;

double L1,L2,alpha,fang,elapseAng,cycleAng,tote_knt;
double cur_load,cur_line,outVolt,vSource,vInput;
double OverLapangle;
int commute,toggle,yes_Entry,modeSw;
FILE *fnew;
char *tstr,*p;



int main(void)
{
 float  ka1,kb2,kc3;
 printf(" \n");
 printf("     Load Time Constant in radians = ");
 scanf("%f",&ka1);
 L1=(double)ka1;
 if (L1<0.05) L1=0.05;
 printf(" \n");
 printf("     Line Reactance Time Constant in radians = ");
 scanf("%f",&kb2);
 L2=(double)kb2;
 printf(" \n");
 printf("     Firing angle in degrees = ");
 scanf("%f",&kc3);
 alpha=(double)kc3;
 fang=alpha*deg_rad;
 alpha=0.0;
 printf("  \n");

 // Initialise though not necessary for global variables

 elapseAng=0.0 ;  cycleAng=0.0;
 cur_load=0.0;  cur_line=0.0;  outVolt=0.0;  tote_knt=0.0;
 OverLapangle=0.0;  commute=0;  yes_Entry=0;


 // Create a file for entering transient response
 fnew=fopen("tran_v1.csv","w+r");
 tranResponse();
 fclose(fnew);
 return 0;
}

void kreateRespFile(void)
{
 int n1,n2;

 tstr="Angle,InputV,VoutBr,LoadCur,LineCur,IndVolt";
 p=strtok(tstr,",");
 fprintf(fnew,p); fprintf(fnew,",");
 n2=6;
 for (n1=0;n1<(n2-1);n1++)
        {
         p=strtok(NULL,",");
         if (n1!=(n2-2))
                {
                 fprintf(fnew,p); fprintf(fnew,",");
                }
         else
                {
                 fprintf(fnew,p); fprintf(fnew,"\n");
                }
        }
}

void tranResponse(void)
{
 double d1;
 int NumCycles,count;
 d1=(6.0*(L1+L2))/(2.0*pi)+0.5;
 NumCycles=(int)d1 + 1;
 kreateRespFile();
 modeSw=1;
 for (count=0;count<=NumCycles;count++)
  OneCycle();
}


void OneCycle(void)
{
 int knt;
 double dknt;
 dknt=0.0;


 for (knt=0;knt<1440;knt++)
        {
         cycleAng=dknt*step;
         vInput=pi/2.0*sin(cycleAng);
         if ((cycleAng<fang) || (cycleAng>(fang+pi)))
                {
                 if (cycleAng<fang) vSource=pi/2.0*sin(cycleAng+pi);
                 else vSource=pi/2.0*sin(cycleAng-pi);
                 toggle=0;
                }
         else
                {
                 vSource=pi/2.0*sin(cycleAng);
                 toggle=1;
                }
         if (modeSw!=toggle)
                {
                 commute=1;
                 if (L2<0.0005) commute=0;
                 modeSw=toggle;
                }
         computeOneStep();
         dknt+=1.0;
        }
}

void computeOneStep(void)
{
 double dLoadI,dLineI;

 switch (commute)
        {
         case 0:
          dLoadI=(vSource-cur_load)/(L1+L2)*step;
          cur_load=cur_load+dLoadI;
          if (cur_load<0.00001) cur_load=0.0;
          if (toggle==0) cur_line=-cur_load;
          else cur_line=cur_load;
          outVolt=cur_load+(vSource-cur_load)*L1/(L1+L2);
         break;

         case 1:
          dLoadI=(0.0-cur_load)/L1*step;
          cur_load=cur_load+dLoadI;
          if (cur_load<0.00001) cur_load=0.0;
          dLineI=vInput/L2*step;
          cur_line=cur_line+dLineI;
          if (toggle==1)
                {
                 if (cur_line>cur_load) commute=0;
                }
          if (toggle==0)
                {
                 if ((cur_line+cur_load)<0.0) commute=0;
                }
          outVolt=0.0;
         break;
        }
 tote_knt+=1.0;
 elapseAng=tote_knt*step;
 alpha=tote_knt/4.0;
 yes_Entry+=1;
 if (yes_Entry==4) produceEntries();
 if (yes_Entry==4) yes_Entry=0;
}

void produceEntries(void)
{
 double negate;
 gcvt(alpha,5,p);
 fprintf(fnew,p);
 fprintf(fnew,",");
 gcvt(vInput,5,p);
 fprintf(fnew,p);
 fprintf(fnew,",");
 gcvt(outVolt,5,p);
 fprintf(fnew,p);
 fprintf(fnew,",");
 gcvt(cur_load,5,p);
 fprintf(fnew,p);
 fprintf(fnew,",");
 gcvt(cur_line,5,p);
 fprintf(fnew,p);
 fprintf(fnew,",");
 if (toggle==0) negate = 1.0; else negate=-1.0;
 gcvt(vInput-negate*outVolt,5,p);
 fprintf(fnew,p);
 fprintf(fnew,"\n");
}
 

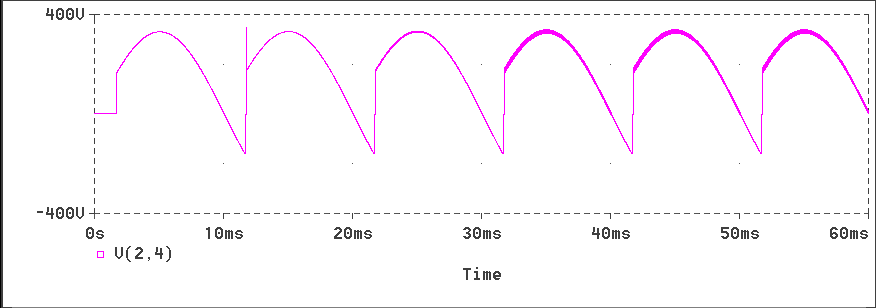
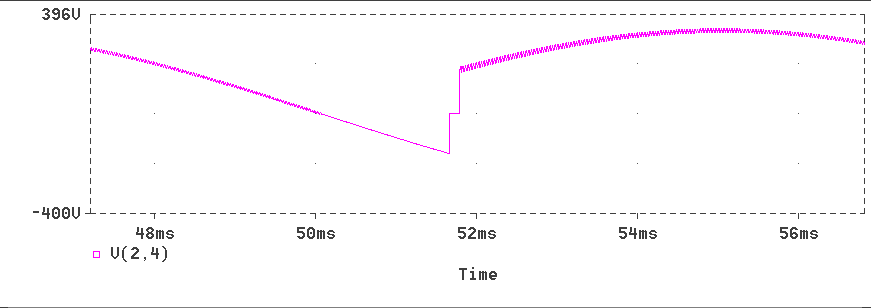
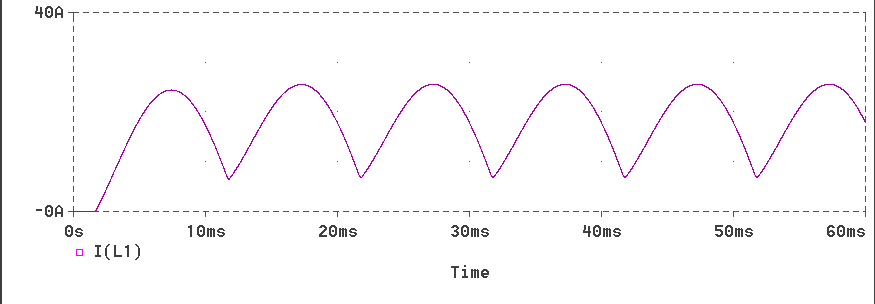
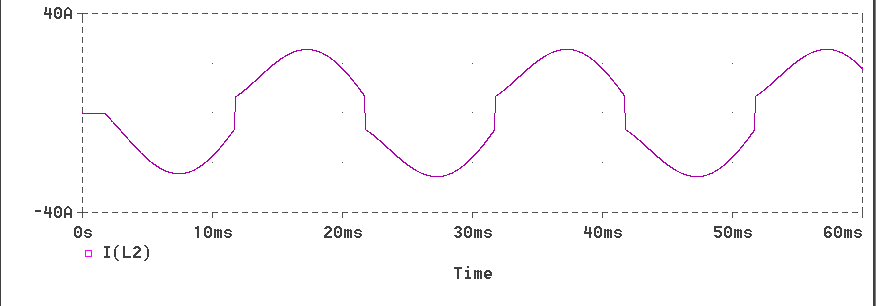
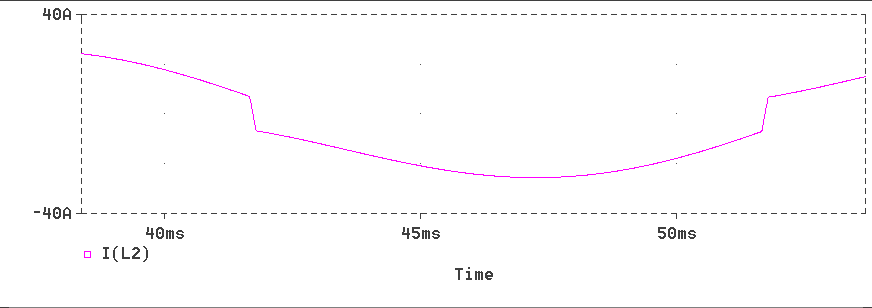
The responses obtained for L1=1.5, L2=0.2 and a = 30o are produced below.

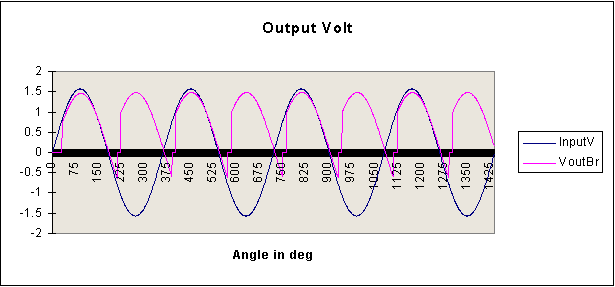
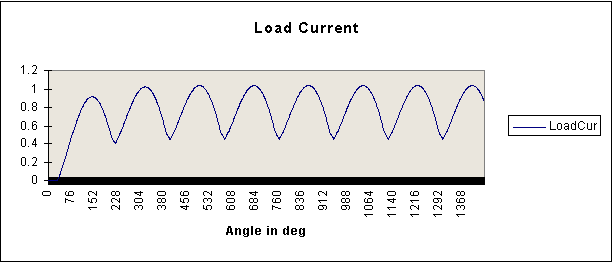
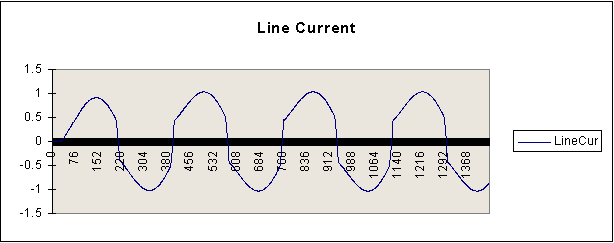
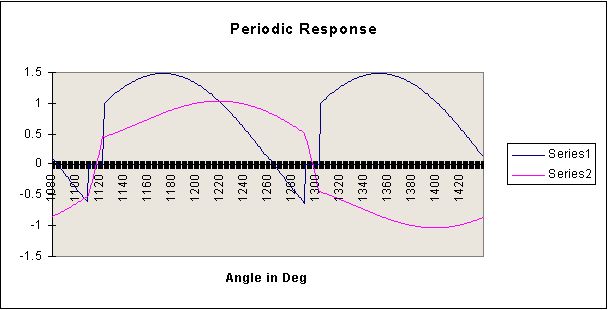
Another C program is presented below.  This program carries out the harmonic analysis. This file, called fcb_1phb.cpp, can be downloaded.   It can also be compiled as a C program.   It produces an output file, called harm_v1.csv.

C Program

// Simulation of a single-phase fully-controlled bridge
// rectifier circuit.
// This program obtainss the periodic response first and
// then computes the ripple components in output current
// and voltage and the harmonic components in the line current.
// The parameters to be fed are just three: the ratio of load
// inductive reactance to the load resistance, wL1/R , the
// ratio of source reactance to the load resistance to load
// resistance wL2/R and the firing angle in degrees.
 
 

#include <math.h>
#include<stdlib.h>
#include<stdio.h>
#include<string.h>

void periodicResponse(void);
void harmonicAnalysis(void);
void OneCycle(void);
void computeOneStep(void);
void kreateRespFile(void);
void produceEntries(void);
 

const double pi=3.1415926;
const double deg_rad=pi/180.0;
const double step=pi/720.0;

double L1,L2,fang,cycleAng;
double cur_load,cur_line,outVolt,vSource,vInput;
double OverLapangle,VoAvg,VoRMS,ILoadAvg,ILoadRMS;
double ILineAvg,ILineRMS,THD,RFVolt,RFCur;
int commute,toggle,modeSw;
double anLoadCur[26],bnLoadCur[26],cnLoadCur[26];
double anLineCur[26],bnLineCur[26],cnLineCur[26];
double anOutVolt[26],bnOutVolt[26],cnOutVolt[26];

FILE *fnew;
char *tstr,*p;
 
 

void main(void)
{
 float  ka1,kb2,kc3;
 printf(" \n");
 printf("     Load Time Constant in radians = ");
 scanf("%f",&ka1);
 L1=(double)ka1;
 if (L1<0.05) L1=0.1;
 printf(" \n");
 printf("     Line Reactance Time Constant in radians = ");
 scanf("%f",&kb2);
 L2=(double)kb2;
 printf(" \n");
 printf("     Firing angle in degrees = ");
 scanf("%f",&kc3);
 fang=deg_rad*(double)kc3;
 printf("  \n");
 

 // Initialise though not necessary for global variables

 cycleAng=0.0;
 cur_load=0.0;  cur_line=0.0;  outVolt=0.0;
 OverLapangle=0.0;  commute=0; modeSw=0;  toggle=0;
 

 // obtain the transient response.
 periodicResponse();
 harmonicAnalysis();
 printf("Close window by clicking on x button at top right corner \n");
}
 

void periodicResponse(void)
{
 double startVal;

 // Calculate one cycle of response and repeat till the
 // response becomes periodic.
 do
        {
         startVal=cur_load;
         OneCycle();
        } while (fabs(startVal-cur_load)>0.0005);
}
 

void OneCycle(void)
{
 int knt;
 double dknt;
 dknt=0.0;

 for (knt=0;knt<1440;knt++)
        {
         cycleAng=dknt*step;
         vInput=pi/2.0*sin(cycleAng);
         if ((cycleAng<fang) || (cycleAng>(fang+pi)))
                {
                  if (cycleAng<fang) vSource=pi/2.0*sin(cycleAng+pi);
                     else vSource=pi/2.0*sin(cycleAng-pi);
                 toggle=0;
                }
         else
                {
                 vSource=pi/2.0*sin(cycleAng);
                 toggle=1;
                }

         // To record commutation overlap, the routine described below is used.
         // When commute is 1, overlap ensues.  It is set to to 1 whenever
         // a pair of SCRs is triggered at the set firing agnle.  It is resset
         // by the compute_one_step routine when overlap ends. This can be
         // checked from the values of load current and line current.

         if (modeSw!=toggle)
                {
                 commute=1;
                 if (L2<0.0005) commute=0;
                 modeSw=toggle;
                }
         computeOneStep();
         dknt+=1.0;
        }
}

void computeOneStep(void)
{
 double dLoadI,dLineI;

 switch (commute)
        {
         case 0:
          dLoadI=(vSource-cur_load)/(L1+L2)*step;
          cur_load=cur_load+dLoadI;
          if (cur_load<0.00001) cur_load=0.0;
          if (toggle==0) cur_line=-cur_load;
          else cur_line=cur_load;
          if (cur_load>0.0) outVolt=cur_load+(vSource-cur_load)*L1/(L1+L2);
          else outVolt=0.0;
         break;

         case 1:
          dLoadI=(0.0-cur_load)/L1*step;
          cur_load=cur_load+dLoadI;
          if (cur_load<0.00001) cur_load=0.0;
          dLineI=vInput/L2*step;
          cur_line=cur_line+dLineI;
          if (toggle==1)
                {
                 if (cur_line>cur_load) commute=0;
                }
          if (toggle==0)
                {
                 if ((cur_line+cur_load)<0.0) commute=0;
                }
          outVolt=0.0;
         break;
        }

}

void harmonicAnalysis(void)
{
 int m;
 double theta,dblm;
 int knt;
 double dknt;
 dknt=0.0;

 for (m=0;m<26;m++)
        {
         anLoadCur[m]=0.0; bnLoadCur[m]=0.0; cnLoadCur[m]=0.0;
         anLineCur[m]=0.0; bnLineCur[m]=0.0; cnLineCur[m]=0.0;
         anOutVolt[m]=0.0; bnOutVolt[m]=0.0; cnOutVolt[m]=0.0;
        }
 

 OverLapangle=0.0;
 ILoadAvg=0.0; ILoadRMS=0.0; RFCur=0.0;
 ILineAvg=0.0; ILineRMS=0.0; THD=0.0;
 VoAvg=0.0;  VoRMS=0.0; RFVolt=0.0;

 for (knt=0;knt<720;knt++)
        {
         cycleAng=dknt*step;
         vInput=pi/2.0*sin(cycleAng);
         if ((cycleAng<fang) || (cycleAng>(fang+pi)))
                {
                 vSource=pi/2.0*sin(cycleAng-pi);
                 toggle=0;
                }
         else
                {
                 vSource=pi/2.0*sin(cycleAng);
                 toggle=1;
                }

         if (modeSw!=toggle)
                {
                 commute=1;
                 if (L2<0.0005) commute=0;
                 modeSw=toggle;
                }
         computeOneStep();

         if ((toggle==1) && (commute==1)) OverLapangle=OverLapangle+step;

         dblm=0.0;
         for (m=0;m<13;m++)
                {
                 theta=2.0*dblm*cycleAng;
                 while (theta>(2.0*pi)) theta=theta-2.0*pi;
                 anLoadCur[2*m]=anLoadCur[2*m]+cur_load*cos(theta)*step;
                 bnLoadCur[2*m]=bnLoadCur[2*m]+cur_load*sin(theta)*step;
                 anOutVolt[2*m]=anOutVolt[2*m]+outVolt*cos(theta)*step;
                 bnOutVolt[2*m]=bnOutVolt[2*m]+outVolt*sin(theta)*step;
                 theta=theta+cycleAng;
                 if (theta>(2.0*pi)) theta=theta-2.0*pi;
                 anLineCur[2*m+1]=anLineCur[2*m+1]+cur_line*cos(theta)*step;
                 bnLineCur[2*m+1]=bnLineCur[2*m+1]+cur_line*sin(theta)*step;
                 dblm=dblm+1.0;
                }

         ILoadRMS=ILoadRMS+cur_load*cur_load*step;
         VoRMS=VoRMS+outVolt*outVolt*step;
         ILineAvg=ILineAvg+fabs(cur_line)*step;
         ILineRMS=ILineRMS+cur_line*cur_line*step;
         dknt+=1.0;
        }

 for (m=0;m<13;m++)
        {
          anLoadCur[2*m]=2.0/pi*anLoadCur[2*m];
          bnLoadCur[2*m]=2.0/pi*bnLoadCur[2*m];
          anOutVolt[2*m]=2.0/pi*anOutVolt[2*m];
          bnOutVolt[2*m]=2.0/pi*bnOutVolt[2*m];
          anLineCur[2*m+1]=2.0/pi*anLineCur[2*m+1];
          bnLineCur[2*m+1]=2.0/pi*bnLineCur[2*m+1];
          cnLoadCur[2*m]=anLoadCur[2*m]*anLoadCur[2*m]
                                                                 + bnLoadCur[2*m]*bnLoadCur[2*m];
          cnLoadCur[2*m]=sqrt(cnLoadCur[2*m]);
          cnLineCur[2*m+1]=anLineCur[2*m+1]*anLineCur[2*m+1]
                                                                + bnLineCur[2*m+1]*bnLineCur[2*m+1];
          cnLineCur[2*m+1]=sqrt(cnLineCur[2*m+1]);
          cnOutVolt[2*m]=anOutVolt[2*m]*anOutVolt[2*m]
                                                                + bnOutVolt[2*m]*bnOutVolt[2*m];
          cnOutVolt[2*m]=sqrt(cnOutVolt[2*m]);
        }
 VoRMS=sqrt(VoRMS/pi);
 ILoadRMS=sqrt(ILoadRMS/pi);
 ILineAvg= ILineAvg/pi;
 ILineRMS= sqrt(ILineRMS/pi);
 ILoadAvg=anLoadCur[0]/2.0;
 VoAvg=anOutVolt[0]/2.0;
 THD=sqrt(ILineRMS*ILineRMS-cnLineCur[0]*cnLineCur[0]/2.0);
 RFVolt=sqrt(VoRMS*VoRMS-VoAvg*VoAvg);
 RFCur=sqrt(ILoadRMS*ILoadRMS-ILoadAvg*ILoadAvg);

 fnew=fopen("harm_v1.csv","w+r");
 kreateRespFile();
 produceEntries();
 fclose(fnew);
}

void kreateRespFile(void)
{
 int n1,n2;
 tstr="harmNo,LoadCur,OutVolt,harmNo,LineCur";
 p=strtok(tstr,",");
 fprintf(fnew,p); fprintf(fnew,",");
 n2=5;
 for (n1=0;n1<(n2-1);n1++)
        {
         p=strtok(NULL,",");
         if (n1!=(n2-2))
                {
                 fprintf(fnew,p); fprintf(fnew,",");
                }
         else
                {
                 fprintf(fnew,p); fprintf(fnew,"\n");
                }
        }
}

void produceEntries(void)
{
 int m;
 for(m=0;m<13;m++)
        {
         itoa(2*m, p, 10);
         fprintf(fnew,p);
         fprintf(fnew,",");

         gcvt(cnLoadCur[2*m],5,p);
         fprintf(fnew,p);
         fprintf(fnew,",");

         gcvt(cnOutVolt[2*m],5,p);
         fprintf(fnew,p);
         fprintf(fnew,",");

         itoa(2*m+1, p, 10);
         fprintf(fnew,p);
         fprintf(fnew,",");

         gcvt(cnLineCur[2*m+1],5,p);
         fprintf(fnew,p);
         fprintf(fnew,"\n");
        }

 fprintf(fnew,"\n");
 p="LoadIAvg";
 fprintf(fnew,p);
 fprintf(fnew,",");
 gcvt(ILoadAvg,5,p);
 fprintf(fnew,p);
 fprintf(fnew,"\n");
 p="LoadIRMS";
 fprintf(fnew,p);
 fprintf(fnew,",");
 gcvt(ILoadRMS,5,p);
 fprintf(fnew,p);
 fprintf(fnew,"\n");
 p="RFCur";
 fprintf(fnew,p);
 fprintf(fnew,",");
 gcvt(RFCur,5,p);
 fprintf(fnew,p);
 fprintf(fnew,"\n");
 fprintf(fnew,"\n");
 

 p="VoAvg";
 fprintf(fnew,p);
 fprintf(fnew,",");
 gcvt(VoAvg,5,p);
 fprintf(fnew,p);
 fprintf(fnew,"\n");
 p="VoRMS";
 fprintf(fnew,p);
 fprintf(fnew,",");
 gcvt(VoRMS,5,p);
 fprintf(fnew,p);
 fprintf(fnew,"\n");
 p="RFVolt";
 fprintf(fnew,p);
 fprintf(fnew,",");
 gcvt(RFVolt,5,p);
 fprintf(fnew,p);
 fprintf(fnew,"\n");
 fprintf(fnew,"\n");
 p="ILineAvg"; fprintf(fnew,p);
 fprintf(fnew,",");
 gcvt(ILineAvg,5,p);
 fprintf(fnew,p);
 fprintf(fnew,"\n");
 p="ILineRMS";
 fprintf(fnew,p);
 fprintf(fnew,",");
 gcvt(ILineRMS,5,p);
 fprintf(fnew,p);
 fprintf(fnew,"\n");
 p="THD";
 fprintf(fnew,p);
 fprintf(fnew,",");
 gcvt(THD,5,p);
 fprintf(fnew,p);
 fprintf(fnew,"\n");
 fprintf(fnew,"\n");

 p="OverLapAngle";
 fprintf(fnew,p);
 fprintf(fnew,",");
 if (OverLapangle>0.0001) OverLapangle=OverLapangle+step/2.0;
 gcvt(OverLapangle,5,p);
 fprintf(fnew,p);
 fprintf(fnew,"\n");

}

The results obtained are presented below.


 
 
 

SUMMARY

This page has described how the fully-controlled bridge rectifier circuit behaves when the source has inductance. In the next page, it is decribed how the operation of this circuit changes  when it has a filter capacitor.

 
GO TO THE TOP OF THE PAGE