AN APPLICATION: A DC POWER SUPPLY
CIRCUIT OPERATION
MATHEMATICAL ANALYSIS
SIMULATION
CIRCUIT OPERATION
A three-phase fully-controlled bridge circuit is a much more suitable circuit to be used for generating a variable dc output voltage than the single-phase fully-controlled bridge circuit, on account of two reasons, which are:
a.    reduced ripple content in its output and
b.    much higher ripple frequency.
Both these factors lead to an LC filter which is relatively small and economical.  This page describes how such a power supply can be built and controlled.
An inductor in the dc link reduces ripple in the output current of the bridge circuit, whereas the capacitor absorbs the ripple in output voltage.  The inductor has to be designed such that it does not saturate even when it carries the maximum current.  This means that it should have an airgap in the path of flux.  The ripple current through the capacitor can also be significant.  Hence it needs to be checked from the datasheet that the capacitor chosen has the required ripple current rating.  For such an application, an electrolytic capacitor is normally chosen and its voltage rating should also be adequate.
We can have a block diagram to describe the operation of this dc power supply obtained using a three-phase fully-controlled bridge rectifier.  The output voltage Vo is varied by varying the firing angle a.  The firing angle in turn is controlled by voltage VC, which is the output of a PI controller.   The inputs to the PI controller are a voltage named Vref representing the desired output voltage and the output voltage Vo of the bridge circuit.  If Vo  is less than the desired output voltage, the resultant error causes the output, VC, to  increase, which in turns should advance firing angle.  As the firing angle is advanced, the output voltage of the bridge circuit increases.  The next section describes how the block diagram can be analysed, leading to simulation of the system.
MATHEMATICAL ANALYSIS

The simulation program is based on the pseudo-code displayed below.

Start block:
    Set the values of load reactance, line reactance, capacitor, load fraction.
    Set the desired output voltage, PI controller parameters
    Set the current firing angle to be 120o.
    Set base reference angle to 60o.
    Set Commute = 0.   ( Indicates no commutation overlap exists at start. )
    Go to Loop Routine.
    Set theta to zero.

Loop Routine
    Call Compute routine.
    Increment theta.
    If {(theta + base reference angle) = (next firing angle) }
       [
        current firing angle = next firing angle.
        base reference angle = next firing angle - 60o.
        Set Commute = 1 .  ( Indicates next SCR is triggered)
      ]
    Execute Loop Routine

Compute Routine:
    If  (Commute == 0)
        [
         compute next value of link inductor current.
       ]
    else
        [
         compute next value of triggered SCR current.
         compute next value of link inductor current.
         if (SCR current link inductor current) Reset Commute to 0.
        ]
    Compute next value of capacitor voltage.
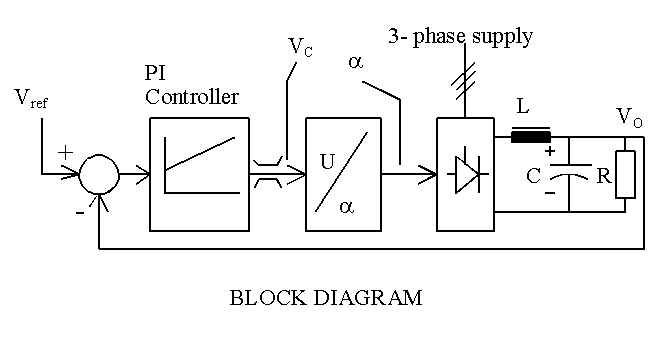
    Compute next value of PI controller's output.
    Compute next firing angle.

The equations used in the Compute Routine are obtained as follows.
 
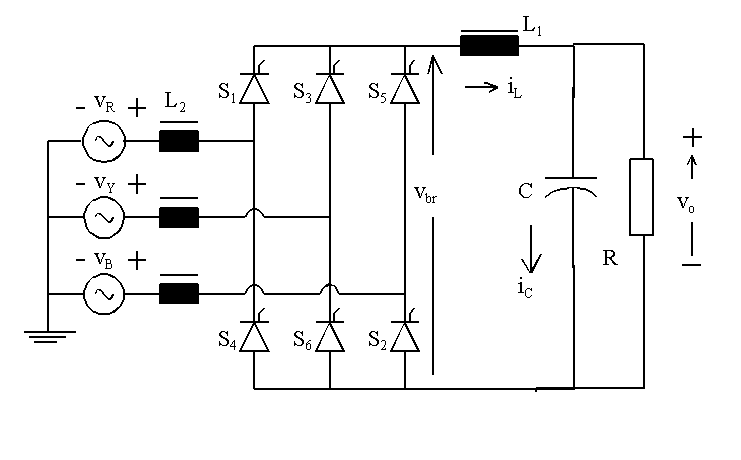
When there is commutation overlap, the output voltage behind the source inductance is expressed by equation (1).  In equation (1),   m is the overlap angle and U is the amplitude of line voltage.  If the output voltage be vo(q) during this period, the differential equation for the current through the dc link inductance is presented as equation (2).  During commutation overlap, the current in the SCR just triggered on is described by equation (3).  The  commutation overlap ends when the current through this SCR equals the dc link inductor current.  When there is no overlap, the bridge output voltage is described by equation (4).

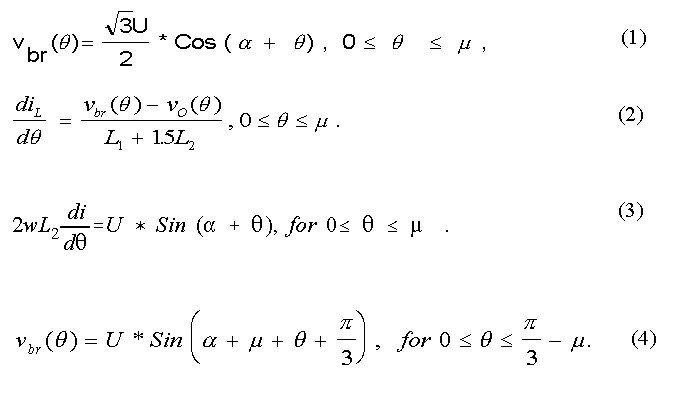
The differential equation that describes the dc link inductor current is then described by equation (5). The differential equation for the capacitor voltage is easily obtained and it is expressed as equation (6). Next the equations relating to closed-loop control are described.  Let the output of PI controller be vC(q) and it is expressed by equation (7). In equation (7), A is a constant to be evaluated, K is the proportional gain of the controller and T is its time constant.  The above equation is represented as equation (8) , which is more convenient for use in simulation. In equation (8), Vref is the desired output voltage.  The output of the controller is normally checked  to ensure that it is within the set limits.  From the output of the controller, the firing angle, a can be obtained.  The maximum output voltage of the controller should correspond to zero degree firing angle and the minimum to 120o firing angle.  Hence we get the following equation for firing angle.  This means that the range for vC(q) is from 0 to VCmax.


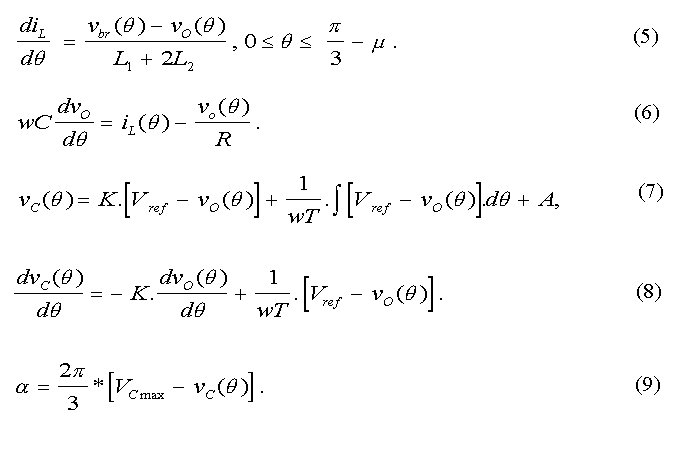
The simulation program uses the above equations and displays the results in a graphical format.
 

SIMULATION

The applet below can be run with the default parameters.  To set any parameter, click on the arrow pointing downwards beside the Peak Source Voltage, a menu would appear. The default value of the parameter highlighted appears in the textfield for Set Value.  To change the parameter, select the parameter and then click within the editable textfield for Set Value.  In order to change this parameter, you must click on Set Value button.  You can set the desired response to be one of three responses.

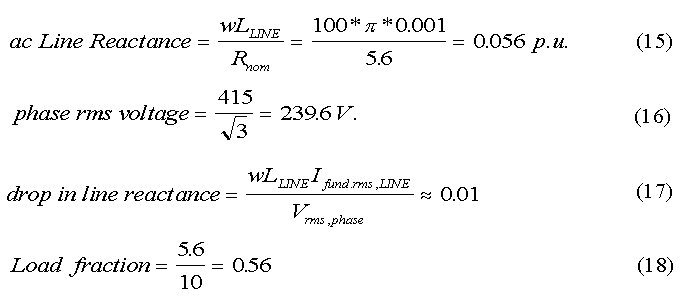
An example is presented now to explain how the per unit values can be set.  Let a 3 phase, 415 V, 50 Hz source supply power to the converter. Then the maximum average voltage that can be obtained is presented in equation (10).  Let the nominal rated dc link current be 100 A.  Then the nominal load resistance or the base impedance for the system is assigned as shown by equation (11).  Given that the current through the load is free of ripple,  the rms line current is obtained according to equation (12) and this value includes  both the fundamental component and the harmonic components.   The fundamental rms component is obtained as illustrated by equation (13). Given that the dc link inductance is 10 mH, its p.u. value is obtained as shown by equation (14).
 


Given that the line inductance is 1 mH, its p.u. value is obtained as shown by equation (16). Usually the line inductance is called as the 4% reactor, implying that when the line current is at its rated value, the rms value of the fundamental component of voltage across the line reactor is 4% of the phase voltage.  For example, if the rms phase voltage is 240 V, the drop across 4% reactor at rated current would be 9.6 V.  When the line voltage is 415 V, the phase voltage is obtained as shown by equation (16). The drop across the line inductor can now be stated as a fraction of the phase voltage as given by equation (17). This means that if the drop across the line inductor is to be 4% of phase voltage, the inductance should be 0.4 mH and not 1 mH.

It is possible to set the load resistance to a value other than its nominal value.  The nominal value of load resistance is 5.6 W.  If the load resistance is to be 10 W, then set Load Fraction as shown by equation (18).
 

 
 

GO TO THE TOP OF THE PAGE